Aerologický výstup

Trocha meteorologické teorie, vysvětlení základních pojmů a principů termiky a vyhodnocení aerologického výstupu.
Článek z čísla 13 časopisu Paragliding

 

    Bez podrobnější znalosti průběhu teploty podél vertikály v atmosféře nemůžeme správně zhodnotit termické podmínky, jaké nás v daný den čekají. Někdy nám dokonce může prostudování diagramu pomoci v rozhodování, zda vůbec má cenu jít létat. Aerologickému diagramu, jak se nazývá graf, zobrazující průběh teploty a rosného bodu s výškou, nelze ovšem přisuzovat absolutní dokonalost - především proto, že jeho měření jeho hodnot probíhá prostřednictvím balónové radiosondy nad jedním určitým místem a podmínky v lokalitě, kde chceme létat a která může být vzdálená od měřícího stanoviště i stovky kilometrů, mohou být poněkud odlišné.

    Vzpomeňme si na dny, kdy přicházejí zprávy od plachtařů v Beskydech o tom, jaké jsou tam vynikající termické podmínky, zatímco třeba v severních Čechách je termika velmi slabá nebo úplně nevyužitelná. Dalším faktorem, který má značný vliv na kvalitu termiky, je samotný terén. Jeho barevné kvality, tepelná kapacita, tvarová proměnlivost a postavení vůči převažujícímu proudění hrají důležitou roli pro vznik a intenzitu termiky, zejména ve spodní části konvektivní vrstvy. Mimo jiné také proto je problematické spočítat z aerologického výstupu rychlost stoupavých proudů. Ta se sice dá odhadnout podle míry instability, ale uvědomme si, že rychlost stoupání termiky je vlastně přetransformovaný přebytek tepelné energie, kterou vzduch získal od přehřátého zemského povrchu. Teplotní rozdíly na nehomogenním terénu jsou však za slunného dne teplé části roku značné. Porovnejme například pokosené obilné pole a sousední louku s nízkou suchou trávou - zde bude těžké určit, který z obou povrchů bude prohřátější a nad kterým tedy vznikne stoupavý proud. Pokud už vznikne, může i nemusí být inteznívní. Záleží na tom, jak velké množství vzduchu (představující energetickou zásobu) se prohřeje, jak dlouho to bude trvat, o kolik bude jedna hmota vzduchu přehřátější oproti té druhé, jak silný bude prvotní impuls, který uvede vzduch do pohybu vzhůru. Naopak, ve skalnatém terénu vysokých hor, kde jsou ostré kontrasty světla a tepla, členitý a prudce svažitý terén, jenž se prohřívá silně nerovnoměrně, nacházíme za slunečných dnů intenzívní a turbulentní termiku velmi často i v zimě, zatímco nad rovinatým krajem není termika vůbec nebo jen slabá. A to přitom obklopuje hory i nepříliš vzdálenou rovinu tatáž vzduchová hmota s tímtéž vertikálním průběhem teploty vzduchu a podobnými parametry vlhkosti. Vzorce pro výpočet vertikální rychlosti termiky berme tedy jen jako velmi orientační s tím, že vždy musíme přihlédnout k tvaru krajiny a k aktuálnímu prohřátí jednotlivých částí zemského povrchu. Zde nastupuje především pilotův cit, zkušenosti a odhad situace.

    Vertikální profily celé řady meteorologických prvků se měří pomocí meteorologického balónu s radiosondou. Je to již letitá, avšak stále účinná metoda měření. Každých 6 hodin se na několika málo observatořích vypustí balón se sondou; jeho výstupná rychlost je stálá a tak se snadno podle doby letu určí, v jaké je sonda výšce. Současně je sonda zaměřována směrovou anténou, jejíž úhlové polohy se odečítají a trigonometricky je tím vypočítán pohyb sondy v třírozměrném prostoru - tak meteorologové obdrží údaj o směru a rychlosti větru v celé troposféře a části stratosféry (sondy běžně dostupují výšky 35 - 50 km nad zemí). Sonda měří teplotu, tlak a vlhkost vzduchu a radiově jí odvysílá. Během zhruba dvouhodinového letu sondy tak získají meteorologové kompletní obraz o průběhu zmíněných meteorologických prvků nad místem měření, resp. nad místy, kam je sonda unášena větrem. Je-li vzduch nucen stoupat vzhůru, například při větru vanoucím přes horský hřeben, dostává se tak do vyšších a vyšších hladin, kde je nižší atmosférický tlak. Stoupající objem vzduchu je tak stále méně stlačován svým vzduchovým okolím a rozpíná se, což má za následek jeho ochlazování. Jinými slovy - stoupající vzduch se ochlazuje. Pokud není nasycený vodní párou, tj. není v něm mlha nebo oblak, ochlazuje se v nižších hladinách asi o 1°C na každých 100 m výšky. Teplota rosného bodu, který je u nenasyceného vzduchu vždy nižší, než samotná teplota, klesá asi o 0,2°C na každých 100 m výšky. Je tedy zřejmé, že se dříve či později obě teploty při stoupajícím vzduchu setkají a vzduch, jehož teplota je totožná s rosným bodem, se nasytí vodní párou - tj. vznikne oblak.

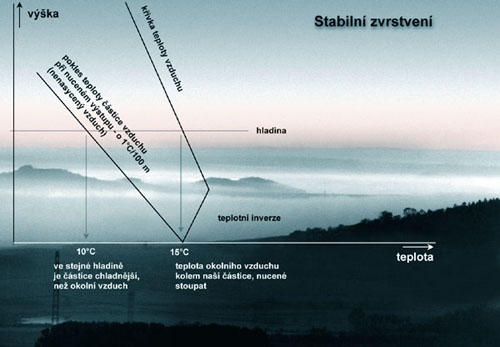
    Představme si situaci, kdy teplota v atmosféře klesá s výškou pomaleji, než o 1°C na každých 100 m. Je-li vzduch nucený stoupat, ochlazuje se (nenasycený) o zmíněný 1°C/100 m a tím pádem čím je výš, tím je chladnější vzhledem ke svému atmosférickému okolí. Jakmile tedy skončí podmínky nuceného výstupu, vrací se vzduchový objem zpátky k zemi, protože studenější vzduch je těžší, než vzduch teplejší (obrázek 1). Za těchto okolností termika nevzniká, popř. může se objevit jen ve vrstvě několika desítek nebo stovek metrů nad zemským povrchem, u něhož dojde vlivem intenzívního slunečního svitu k výraznějšímu přehřátí a tudíž dočasné labilitě. S těmito situacemi se nejčastěji setkáme v babím létě koncem srpna, v září a v říjnu, kdy k nám ve vyšších hladinách často proudí teplejší vzduch od jihu až jihozápadu a utvářejí se už výrazné teplotní inverze. Při jejich částečném odbourávání v poledních hodinách se může labilizovat poměrně tenká vrstva vzduchu nad zemí a zejména s padákovými kluzáky pak můžeme místně využívat slabé termiky.

    Po kliknutí se zvětšíJestliže teplota vzduchu v atmosféře klesá s rostoucí výškou o více než 1°C / 100 m, nabývá nuceně vystupující částice stále vyšší teploty oproti svému okolí. Tím se také stává lehčí než vzduch, který ji obklopuje a posléze už k výstupnému pohybu nepotřebuje žádný "donucovací prostředek", jakým je například vítr vanoucí nahoru po horské stráni a stoupá sama. Tento stav se nazývá absolutní instabilita nebo také absolutní labilita v atmosféře a je základní podmínkou pro vznik termiky. Ještě bych chtěl zmínit jakýsi mezistav, při němž je vertikální profil teploty stabilní při nenasyceném (suchém) vzduchu, avšak již instabilní při nasyceném vzduchu. Jak je to možné? Protože pokud dochází ke kondenzaci vodní páry, například při vzniku kupovitého nebo jakéhokoliv jiného oblaku, uvolňuje se přitom tzv. skryté neboli latentní teplo, které poněkud zmírňuje pokles teploty vystupující částice. Ve vzduchu nasyceném vodní párou tak klesá teplota vystupující částice pouze asi o 0,6°C/ 100 m výšky. Představme si nyní situaci, kdy teplota okolní atmosféry klesá o 0,8°C/ 100 m. Pro nenasycený vzduch je to stabilní zvrstvení (tj. stabilní vertikální teplotní gradient), avšak pro nasycený vzduch je tento teplotní profil již instabilní. Když v takovéto situaci nuceně stoupá vzduch podél horského svahu nahoru, termika nevzniká, dokud nedosáhne kondenzační hladiny; potom se stoupající vzduch rázem stane instabilní a stoupá i bez přičinění větru. Tím může vznikat v horách mohutná kupovitá oblačnost, třeba i v nočních hodinách a lehce může dojít ke vzniku bouřek. Co tedy vyčteme z aerologického výstupu? Předně se budeme zajímat, zda je zvrstvení stabilní či instabilní, popřípadě zda je vůbec předpoklad nějaké instability. Pro Českou republiku lze diagram získat prostřednictvím internetových stránek Českého hydrometeorologického ústavu, kde je k dispozici 4x denně výstup z Prahy - Libuše. V tomto diagramu je zakreslena nenasycená adiabata - to je právě křivka, podle které se mění teplota vystupující částice vzduchu s výškou; uváděli jsme, že je to přibližně 1°C/100 m. Tato hodnota se s rostoucí výškou mění, ale pro naše účely postačuje uvažovat jí jako konstantu. Z teploty rosného bodu je vedena čára specifické vlhkosti, která znázorňuje pokles teploty o 0,2°C/ 100 m výšky, což je změna teploty rosného bodu. Rosný bod je teplota, na níž bychom museli vzduch izobaricky ochladit, aby se nasytil vodní párou. Pohled na obrázek 2 ukazuje, jak se s rostoucí výškou obě křivky (nenasycená adiabata i křivka specifické vlhkosti) k sobě přibližují, až se konečně protnou. To je místo, kde teplota stoupající částice vzduchu dosáhne rosného bodu a tím pádem začne kondenzovat pára, tj. vznikne kupovitý oblak. Výšku, v níž dojde k tomuto ztotožnění obou teplot, se nazývá konvektivní kondenzační hladina (KKH). Ke vzniku termiky však je nezbytně nutné, aby zvrstvení bylo instabilní, tj. aby teplota okolní atmosféry klesala s výškou alespoň o 1°C/ 100 m. Tohoto stavu bude dosaženo, když teplota při zemi vystoupí na tzv. konvektivní teplotu Tk, kterou zjistíme, spustíme-li z KKH nenasycenou adiabatu k zemskému povrchu. Porovnejme tuto zjištěnou teplotu s předpovídaným teplotním maximem pro příslušný den! Říká předpověď, že teplota vzduchu bude vyšší, než Tk? Pokud ano, lze očekávat, že bude termický den. Máme-li dobrý odhad, v kolik hodin dosáhne teplota vzduchu hodnoty Tk na své stoupající části křivky denního průběhu a současně v kolik hodin klesne pod Tk při sestupu v odpoledních nebo večerních hodinách, obdržíme časový interval, v němž bude existovat termika. Příklad: Zjistili jsme, že konvektivní teplota Tk je 15°C. Předpověď udává, že nejvyšší denní teploty budou dnes 27°C. V 8 hodin ráno (je polovina srpna) je teplota 10°C a my můžeme odhadovat, že Tk bude dosaženo zhruba kolem 10.hodiny ranní. Maxima 27°C může být dosaženo okolo 14.hodiny a odpolední pokles teploty bude při skoro jasné obloze celkem pomalý; teploty 15°C dosáhne vzduch opět kolem 18.hodiny. Máme tedy k dispozici čas od 10 do 18 hodin, tj. 8 hodin, kdy můžeme využívat termiku. Její kvality a intenzita se samozřejmě během dne mění, hned v 10 hodin jistě nebude ještě natolik rozvinutá, abychom s její pomocí mohli letět klasický přelet. Počítejme s tím, že skutečně využitelná začne být v uvedeném příkladu až asi ve 12 hodin a zeslábne kolem 16.30. Faktický časový interval kvalitní termiky je tudíž 4,5 hodiny. Počítáme-li s časovou rezervou 1,5 hodiny (během přeletu můžeme narazit na nečekané problémy), zbývají nám na uletění nějaké trati jen 3 hodiny. Při bezvětří a průměrných termických podmínkách počítejme traťovou rychlost padáku asi 20 km/h, takže reálná možnost pro cílový let je 60 km.

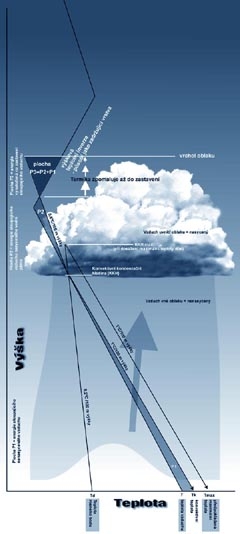
    Vraťme se k aerologickému výstupu. Stoupající vzduch bude po dosažení KKH měnit svoji teplotu podle nasycené adiabaty, tj. o 0,6°C/ 100 m. Dokud trvají podmínky pro samovolný výstup, vzduch v termice stoupá. Pokud chybí zadržující vrstva v podobě výškové inverze, stoupá termika až vysoko do troposféry, ba i do stratosféry a pak je tu vysoká pravděpodobnost vzniku bouřek. Pokud existuje výrazná výšková inverze, jako je tomu na obrázku 2, dochází k postupnému setření rozdílu teplot mezi vzduchem v termice a vzduchem v okolí stoupavého proudu, takže se termika zpomaluje, až se zastaví docela. V jaké výšce to bude? Podívejme se znovu na obrázek 2. Křivka teploty vzduchu spolu s nenasycenou adiabatou a zemským povrchem vymezují formální plochu P1, reprezentující energetický integrál kinetické energie stoupajícího nenasyceného vzduchu. Aplikujeme-li tuto energii do praxe s ohledem na empirické opravné konstanty zejména na tření vzduchu, získáme odhad vertikální rychlosti termiky v té části konvektivní vrstvy, která se nachází pod KKH. Upozorňuji však, že vlivy nehomogenity teplotního pole zemského povrchu jsou natolik rozptýlené hodnoty, že často mohou být takovéto odhady velmi zavádějící. Nad KKH vidíme na obrázku 2 plochu P2, která je vymezena křivkou teploty vzduchu a nasycenou adiabatou. Součet ploch P1 a P2 je souhrnná urychlující energie termického stoupavého proudu a protože platí zákon zachování energie, selskými počty můžeme snadno uvážit, že kolik energie termika spotřebuje na svůj pohyb vzhůru, tolik je potřeba k jejímu zastavení v zadržující vrstvě. Proto určíme plochu P3, která je stejně velká, jako P1+P2, avšak na druhé straně teplotní křivky. Ve skutečnosti to takhle jednoduché a idealizované není, především proto, že vzduch stoupající v termice není izolován vůči svému okolí, s nímž si vesele vyměňuje zejména teplo. Vrcholy oblaků, jejichž výšku obdržíme konstrukcí energetických ploch, pak vycházejí poněkud zkresleně, ale tato odchylka není zpravidla nějak zvlášť významná. Stoupavý proud je zpravidla nejsilnější ve svém středu v tzv. jádru. Teplota vzduchu je tam nejvyšší, neboť čím blíže k okraji stoupavého proudu, tím více se turbulentními pohyby mísí vzduch v termice se vzduchem v jejím okolí. Při okraji stoupavého proudu je tedy vzduch chladnější, pomaleji stoupající a také vlhčí. Proto například bývají základny kumulů, pod nimiž je aktivní stoupavý proud, mírně prohnuté dovnitř - vzduch uprostřed termického proudu je sušší a ke kondenzaci tedy dochází později ve větší výšce, než při okrajích termiky. Pokud se KKH nachází teoreticky nad zádržnou vrstvou, ke vzniku kupovitého oblaku vůbec nedojde, ač jinak může termika existovat. Taková termika se nazývá bezoblačná a u nás bývá často v centrálních částech letní anticyklóny nebo při větru z východního sektoru, kdy je k nám přinášen suchý a horký pevninský vzduch. Podle tvaru kumulů lze také usuzovat řadu zajímavostí o kvalitě termiky.

Petr Dvořák