Aerologický výstup
Hezky psaný a snadno pochopitelný článek o vyhodnocování aerologického výstupu.
Ukázka z knihy Meteorologie pro plachtaře, která vyjde v nakladatelství
Grada Publishing v červnu nebo červenci 1998.
Zveřejněno s laskavým svolením nakladatelství Grada Publ.,s.r.o.
Podívejme se na teplotu vzduchu pohledem Archimédova zákona, který v podstatě vysvětluje termiku. Víme, že ponoříme-li do tekutiny těleso o určitém objemu, je nadlehčováno silou, odpovídající hmotnosti oné tekutiny tímto tělesem vytlačené. Meteorolog k tomu dodává, že tou tekutinou, do níž noříme těleso, je atmosféra, a samotné těleso je - klidně kus vzduchu. Nemusíme hned pochybovat o takové úvaze, protože si představme vzduchovou bublinu, jejíž některé parametry, hlavně teplota, se liší od atmosféry, která tuto bublinu obklopuje. Navíc budeme předpokládat jakousi teplotní izolovanost naší bubliny vůči jejímu okolí, takže si teoreticky nebude své teplo s okolím vyměňovat. Jinak řečeno, pokud se bude její teplota měnit, nebude toho příčinou vzduch, který ji obklopuje. Teplota bubliny se pak bude měnit pouze vlivem jejího rozpínání nebo stlačování -podle toho, jestli bude atmosférou stoupat nebo klesat, a tyto změny teploty se nazývají adiabatické.
Vezměme bublinu vzduchu a zahřejme jí. Teplejší vzduch je řidší a lehčí, než vzduch chladnější. Mírně zahřátá bublina začne sama stoupat vzhůru. Zkusme si hned malou početní úvahu. Nechť naše bublina má stejně jako vzduch, jenž jí obklopuje, teplotu 15oC, to je 288 Kelvinů. Pak nechme zasvítit slunce na louku, u jejíhož povrchu se bublina vzduchu povaluje. Slunce zahřeje zemský povrch a ten zase zahřeje bublinu. Nechť jí oteplí o dva stupně Celsia, na hodnotu 17oC (290 K). Druhý Newtonův zákon síly nám dává odpověď, s jakým vertikálním zrychlením začne bublina stoupat vzhůru:
a = g. (T1-T2)/T2
kde a je zrychlení
g je gravitační konstanta 9.82 m/s2
T1 je teplota bubliny
T2 je teplota okolního vzduchu
Když dosadíme číselné hodnoty, obdržíme:
a = 9.82 (290 - 288)/288
tedy a = 0.07 m/s2
Pokud by naše předepsané podmínky trvaly i podél vertikály, kudy bublina začala stoupat, měla by už po pouhé minutě stoupání rychlost přes 4 m/s a byla by ve výšce asi 130 metrů nad zemí. Základní podmínkou, aby bublina stále mohla stoupat, je to, že bude podle Archimédova zákona neustále nadlehčována. Musí být teplejší, než okolní vzduch. Podívejme se proto na průběh teploty vzduchu, který bublinu obklopuje, jinak řečeno, na vertikální teplotní gradient atmosféry - teplotní zvrstvení. Sama bublina se při svém výstupu vlivem klesajícího atmosférického tlaku rozpíná a tím ochlazuje; můžeme říci, že asi o 1oC na každých 100 metrů výšky. Předpokládáme vzduch, který zatím není nasycený vodní párou. Jestliže se úplně stejně ochlazuje s narůstající výškou i sama atmosféra, nebude se teplota bubliny vlastně nikde lišit od teploty okolního vzduchu. Můžeme bublinu posunout kamkoliv, a ona tam bude stejně těžká, jako atmosféra, která jí obklopuje. Proto nebude bublina ani klesat, ani samovolně stoupat a my nazveme toto zvrstvení atmosféry jako indiferentní. Případ, kdy teplota atmosféry klesá pomaleji, než teplota bubliny, má za důsledek toto: čím vytlačíme bublinu výš, tím bude vůči svému okolí chladnější. Když jí přestaneme nutit k výstupu, okamžitě sama začne klesat dolů, protože jakožto studenější má vyšší hmotnost, než okolní atmosféra. Tato situace se v naší přírodě objevuje dost často - třeba na podzim a v zimě, kdy se česká kotlina zaplní studeným vzduchem při inverzi teploty. Už slovo inverze říká, že teplota vzduchu s narůstající výškou narůstá, zatímco teplota nuceně vystupující bubliny adiabaticky klesá o jeden stupeň Celsia na každých nastoupaných sto metrů výšky. Je jasné, že při inverzi nebo izotermii opravdu nemůže nastat samovolný výstup vzduchové částice a termika není možná. Pomyslná vzduchová bublina je stabilně "držena při zemi" a proto nazýváme teplotní zvrstvení, při kterém je vertikální gradient teploty vzduchu nižší než 1oC/100 m jako stabilní. Pokud ale teplota vzduchu klesá rychleji, než jeden stupeň Celsia na sto metrů výšky, bude teplota bubliny při jejím výstupu vyšší, než teplota okolního vzduchu. Bublina bude sama stoupat až do výšky, v níž jí změna teplotních poměrů nezabrzdí. Tento vertikální teplotní gradient nazýváme instabilní nebo labilní. Labilita atmosféry je základním předpokladem pro rozvoj termiky.
Je však rozdíl mezi ochlazováním vystupující částice vzduchu, která není nasycená vodní párou, a tou, v níž už k nasycení došlo. Nenasycený stoupající vzduch je například hluboko pod základnami kumulů; jakmile dostoupá do kondenzační hladiny, dojde k jeho nasycení a ke vzniku kupovitého oblaku. Při kondenzaci se uvolňuje jisté množství latentního tepla, díky kterému se stoupající bublina ochlazuje o něco pomaleji. Ochlazování vystupujícího nasyceného vzduchu je v tom případě jen 0.6oC/100 m výšky. A nyní si představme, že teplota atmosféry se ochlazuje o 0.8 stupně na každých sto metrů. Kdybychom do ní umístili nenasycený vzduch, samovolně by rozhodně nestoupal, protože takový vertikální teplotní gradient by byl pro něj stabilní. Kdybychom však bublinu nasytili vodní párou, pak by vůči ní byla atmosféra už instabilní! Takové případy se opravdu stávají - představme si, jak fouká vítr přes pohoří, takže nenasycený vzduch je nucený vystupovat přes kopce vzhůru. Jak se při výstupu ochlazuje, dojde k jeho kondenzaci a poté už stoupá nikoliv nuceně, nýbrž samovolně. Někdy se takto můžou v horských oblastech utvářet večerní a noční bouřky. Tento typ zvrstvení se nazývá podmíněná instabilita.
Adiabatické procesy v atmosféře
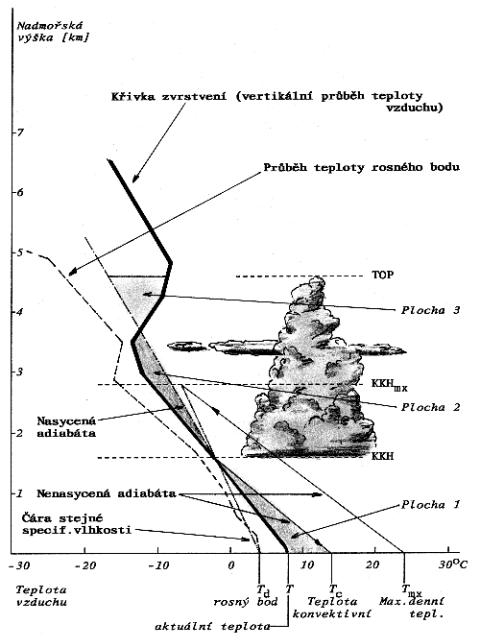
Zde bychom si měli teoreticky popsat výstup vzduchové bubliny při termickém počasí a objasnit, co se děje s vystupujícím teplým vzduchem v termice a známe-li výškový profil teploty okolního vzduchu a průběh atmosférické vlhkosti, co z toho můžeme vyvodit. V první řadě udělejme zjednodušenou úvahu a předpokládejme, i když to v praxi není tak docela pravda, že vzduch ve stoupající termické bublině se nemísí se vzduchem, který ji obklopuje. Když dojde k jejímu přehřátí vůči okolnímu vzduchu, bude mít tendenci podle Archimédova zákona stoupat. Zrychlení a samotná rychlost jejího pohybu vzhůru bude úměrné teplotnímu rozdílu bubliny a okolní atmosféry, což je na první pohled zřejmé - čím teplejší bublina a čím studenější atmosféra, tím větší vztlaková síla nutí bublinu stoupat. Posuďme pohyb bubliny pomocí energie: teplotní rozdíl ve prospěch bubliny znamená, že tato bublina má přebytek tepelné energie oproti atmosféře, a tuto tepelnou energii pak může přeměnit v energii pohybovou. Naše bublina se začne pohybovat vzhůru, a tento pohyb trvá tak dlouho, dokud trvá její převaha tepelné energie. Velikost této energie můžeme spočítat pomocí rovnice anebo odečíst z grafu, který zobrazuje vertikální průběh teploty vzduchu a vlhkosti (obrázek).

Graf se nazývá aerologický diagram, jeho vodorovnou osu tvoří teplotní škála a svislou osu některá veličina, která nám dobře poslouží jako vertikální souřadnice. Může to být například výšková stupnice. Proveďme si malý rozbor obrázku. Tlustou čárou je zobrazený průběh teploty s výškou. Je to tzv. křivka zvrstvení. Přerušovaná čára ukazuje průběh teploty rosného bodu a tak vidíme, jaký je rozdíl obou teplot v různých výškách. Tam, kde jsou obě čáry u sebe blíže, je vyšší poměrná vlhkost vzduchu. Čára, kterou v grafu vedeme z teploty rosného bodu na úrovni zemského povrchu, je tzv. čára stejné specifické vlhkosti vzduchu, je to také křivka průběhu teploty, a ukazuje nám, o kolik bychom museli snižovat při adiabatickém výstupu teplotu bubliny, aby se v ní zachovávala stále stejná specifická vlhkost. Hodnota jejího poklesu s výškou je zhruba 0.2 stupně Celsia na každých 100 metrů. Veďme tuto čáru z teploty rosného bodu vzhůru až do místa, kde protne křivku zvrstvení. Právě v této hladině bude ležet při aktuální teplotě vzduchu T, z níž vychází křivka zvrstvení, konvektivní kondenzační hladina KKH - jinými slovy základny kumulů. Spusťme z KKH šikmo dolů nenasycenou adiabatu, která znázorňuje změny teploty bubliny ještě předtím, než se nasytí v KKH vlhkostí. Průsečík nenasycené adiabaty s úrovní zemského povrchu je údaj o konvektivní teplotě, tj. teplotě, při níž začne fungovat termická konvekce. Pokud během dne vyšplhá rtuť teploměru na tuto hodnotu nebo i výš, pak předpovídáme vznik termiky. Je to jeden z předpokladů její existence. Dalším nezbytným předpokladem je instabilita teplotního zvrstvení.
A teď to důležité: plocha, kterou vymezuje na našem diagramu křivka zvrstvení, nenasycená adiabata (také nazývaná stavová křivka) a hladina nadmořské výšky příslušného zemského povrchu, odpovídá kinetické energii vystupující bubliny nebo správněji vzduchové částice v oblasti mezi zemí a základnou kumulů. Označme si jí zde jako PLOCHA 1. Pokud je stavová křivka vpravo od křivky zvrstvení tak jako na našem obrázku, je energie částice kladná a bublina tak bude na základě archimédovských sil nucena samovolně stoupat. Když vystoupá až do KKH, dojde ke kondenzaci vodní páry a vzniku kupovitého oblaku. Pokud bude částice pokračovat ve svém výstupu, bude se nyní ochlazovat jen o 0.6oC/100 metrů díky uvolňování latentního tepla při kondenzaci páry. Jestli mají být splněny podmínky pro další stoupání bubliny, musí teplota okolní atmosféry klesat s výškou o více než těchto 0.6 stupně Celsia na každých sto metrů. Čáru tohoto poklesu jsme zakreslili v diagramu z průsečíku křivek zvrstvení, čáry stejné specifické vlhkosti, nenasycené adiabaty a KKH. Stoupejme pohledem po této nové čáře, která se jmenuje nasycená adiabata až do bodu, kde znovu protne křivku zvrstvení. A opět nám tak vymezuje plochu, danou nasycenou adiabatou a křivkou zvrstvení, kterou jsme označili jako PLOCHA 2 a ta odpovídá kinetické energii stoupající částice, nyní již nasycené vodní párou. Protože je na našem obrázku zase stavová křivka - teď je stavovou křivkou nasycená adiabata 0.6oC/100 m vpravo od křivky zvrstvení, je opět kinetická energie daná touto plochou kladná a to znamená, že i tady je naší bublině udíleno zrychlení směrem vzhůru.
Ono by to bylo ve skutečnosti pěkné, protože stoupavý proud by se podle této teorie se vzrůstající výškou nad zemí neustále zrychloval a pod základnami kumulů by nám ulítly ručičky variometru. Jak to, že tomu tak v praxi není? Kdo zkusil někdy vypustit pouťový balónek, už tuší odpověď. Balónek se stejně jako vzduchová termická bublina prodírá okolní atmosférou, která jí vlastně třením brzdí- jako loďka, která jede vodou. A to stále neuvažujeme, že by se mohl do stoupající termiky vměšovat chladnější vzduch z okolí. Takže energie stoupavého proudu je poněkud rozptylována třením vzduchu o vzduch a bublina stoupá víceméně rovnoměrně a nezrychleně. Teprve ve výšce, kde nasycená adiabata protíná křivku zvrstvení, končí zároveň zásoba kladné energie, která byla doposud hnacím motorem termické bubliny, a ve výškách nad touto hladinou začíná být pohybová energie vystupující částice záporná. To znamená, že jí začíná brzdit. A protože platí zákon zachování energie, budeme uvažovat, že k úplnému zastavení termické bubliny bude zapotřebí téže energie, kterou bublina potřebovala k udílení svého pohybu vzhůru. Tak zkonstruujeme plochu označenou PLOCHA 3, jejíž velikost musí být stejná, jako součet obou ploch kladných energií PLOCHA 1 a PLOCHA 2. Třetí plocha bude také vymezená křivkou zvrstvení, nasycenou adiabatou, protože předpokládáme, že stoupavý proud bude zpomalovat uvnitř kupovitého oblaku, tedy tam, kde je vzduch nasycený párou, a vodorovnou přímkou, určující nám hladinu, v níž se termická bublina zastaví. Tím jsme stanovili výšku dostupu termických stoupavých proudů a vlastně výšku vrcholů kumulů a tloušťku celé konvektivní vrstvy.
Když známe předpověď maximální denní teploty, můžeme si tuto hodnotu Tmx zakreslit do diagramu, vést z ní nenasycenou adiabatu a stanovit výšku základny kumulů při dosažení této teploty. Z obrázku vidíme, že KKH při teplotě Tmx leží výš, než při T. Z toho poznáváme, že základny kupovitých mraků během dne zvyšují svojí výšku nad zemí a někdy se můžou dokonce přiblížit až do výšky vrcholků kumulů. Oblaky tak mohou zmenšovat svůj vertikální rozměr a přecházet postupně na typ humilis a můžou během dne úplně vymizet. Termika může existovat nadále, jenom už není provázena konvektivní oblačností.
Uvedená metoda aerologického rozboru se nazývá metoda částice, ovšem prokazuje některé nedostatky, jichž jsme se při výkladu dotkli. Předně uvažuje naprostou energetickou izolovanost stoupající termické bubliny od okolní atmosféry. V reálné přírodě je tomu ale jinak - bublina část své energie ztrácí, protože odevzdává trochu svého přebytku tepla do okolního vzduchu. Pak je ale jasné, že její kladná energie nebude tak velká, aby dokázala bublinu transportovat do tak velké výšky, kterou jsme zjistili pomocí porovnání kladných a záporných ploch. Můžeme říci, že metoda částice nadhodnocuje jak výšku dostupu termických stoupavých proudů, tak i samotnou jejich energii, potažmo - rychlost stoupání. Ani absolutní vlhkost si bublina nezachovává. Vlivem turbulentní výměny při okrajích stoupavého proudu se do bubliny dostává více vlhkosti z okolního vzduchu a okrajové části stoupavých proudů tak provází dřívější vznik oblaku cumulus, než v centru proudu. Proto jsou základny kumulů u aktivní termiky uprostřed mírně prohnuté směrem dovnitř oblaku. V meteorologické praxi se teoretický výpočet aerologických parametrů ještě opravuje o vliv okolí na částici. Jedná se o metodu vtahování, jíž se podrobněji zabývat nebudeme.
Jiná metoda aerologického rozboru se nazývá metoda vrstvy a na rozdíl od metody částice bere v úvahu nejen stoupání termických bublin, ale i kompenzační klesavé proudy, které nahrazují vzduch v termice, odtržený od zemského povrchu a stoupající vzhůru. Energie klesavých proudů potom dost výrazně redukuje původně vypočtenou energii stoupající bubliny, a to asi na čtvrtinu hodnoty, kterou udává metoda částice. Z metody vrstvy vyplývají některé fyzikální vzorce pro výpočet množství konvektivní oblačnosti a rychlostí stoupání, ovšem výsledky výpočtů jsou oproti praxi značně nepřesné.